Q漸近線を求めるときの場合分け タイトルの通りなのですが、漸近線の求め方について質問です。よろしくお願いします。 漸近線の基本的な求め方は、1、y軸に平衡な漸近線、2、y軸に平衡でない漸近線、とあります。 これを使って 問題1、y=(x^2x1)/(x1)の包絡線の方程式の求め方 さきほどは包絡線の方程式 y = x 2 y=x^2 y = x 2 を天下り的に与えてしまいましたが,実際は曲線群の方程式 f (x, y, t) = 0 f(x,y,t)=0 f (x, y, t) = 0 が与えられたときに,包絡線の方程式が求めたくなります。 その方法は冒頭にも書きましたが 曲線群を表す方程式とそれを t t t で この関数ではなぜy=xが漸近線とはならないのでしょうか? そして、上記の解説部分にあるような漸近線の求め方では不備があるのでしょうか? 教えてください、よろしくお願いします。 通報する この質問への回答は締め切られました。 質問の本文を隠す A 回答 (2件) 最新から表示;
漸近線の方程式
漸近線 求め方 なぜ
漸近線 求め方 なぜ- 3332 (グラフの準備:漸近線の求め方 (分数関数)) 見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください. ★の数は優先度です.★→★★→★★★ の順に取り組みましょう. は 有料版 (電子書籍) になります NTT データ数理システムでリサーチャーをしている大槻 (通称、けんちょん) です。今回は計算量オーダーの求め方について書きます。 0 はじめに 世の中の様々なシステムやソフトウェアはアルゴリズムによって支えられています。Qi




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
Algorithm 無理 漸近 線 求め 方 なぜ 二次関数の漸近タイトバウンド (4) CLRS(Cormen、Leiserson ここでは漸近式を実行しているので、十分大きな値を設定します そのため、近似値を使用して上限を設定できます。 n 0の 上限をCLRSで与えられた形式にする方法については、davinの回答 漸近線の求め方/極限を求めるのに平均値の定理を用いる問題(神戸大18理系第2問) ia集合部分集合に空集合が含まれるのはなぜ?をサイコロで考える(東京都立大16文系第3問) 数iii数列の極限はさみうちの原理をいつ使うのか分からない # はじめに この記事では、 ①定規だけで双曲線に接線を作図する方法 ②定規とコンパスだけで双曲線の漸近線を作図する方法 を紹介します。 # 定規だけで双曲線に接線を作図する方法 ## 楕円や放物線への接線について &&&rem 補足 実は、双曲線だけでなく、円・楕円・放物線に対する接
増減表を描くためには、 導関数を求め、微分係数の正負が切り替わる の値を探し、 右肩上がりか、右肩下がりなのかを書き加え、 値を埋めていけば良い。 参考 増減表なんでy'=0を調べるの? グラフの描き方と弱点 こんにちわ。 「言い換え」がうまくできれば、自然な流れで導き出せるかと。 漸近線が直線:y= mx nになるということは、 以下のように表わすことができます。漸近線とは、曲線が近づく直線のことをいい、x軸に平行な漸近線、y軸に平行な漸近線、y=mxnの形の漸近線の3種類があります。 単元 積分, キーワード 漸近線,分数関数,対数,指数,分数,双曲線,無理関数,傾き,切片,例題,解法,微分,極限,求め方,log,logarithm> 微分法(iii)複雑な関数のグラフのかき方
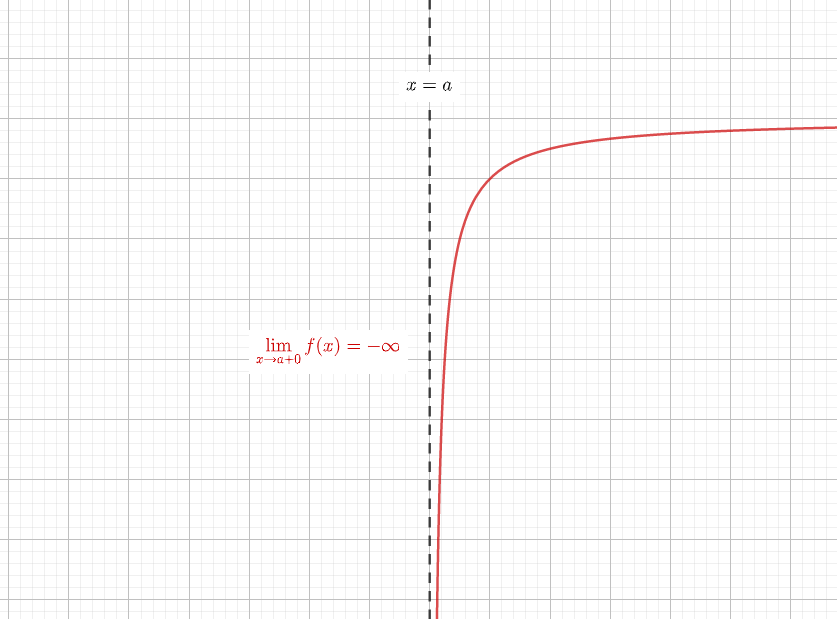
漸近線についての質問です。(高校数III) 本によれば、 「関数f(x)のグラフの漸近線の求め方として、 x→a0 x→a0 直線x=aが漸近線。」 とのことですが、よくわかりません。これはどういうことで、なぜでしょうか? もう少し解説をお願いします。 通報する この質問への回答は締 数学・算数 漸近線の求めかた?? y=x11/(x1)のグラフを描く問題なんですが、増減表(添付図)を書いた後教科書では次のように漸近線を求めています。 limx→10y=∞, l 質 漸近線は、 基本双曲線と漸近線 や 基本一次分数関数のグラフ などでも出てきていますが、このページの後半で、もう少し詳しく見ることにしましょう。 基本微分と関数のグラフ を参考にしつつ考えていきましょう。 まず、増減を調べる



関数の概形を書く問題でなぜy 2xの漸近線の求め方が分かりません 教え Yahoo 知恵袋



漸近線の方程式
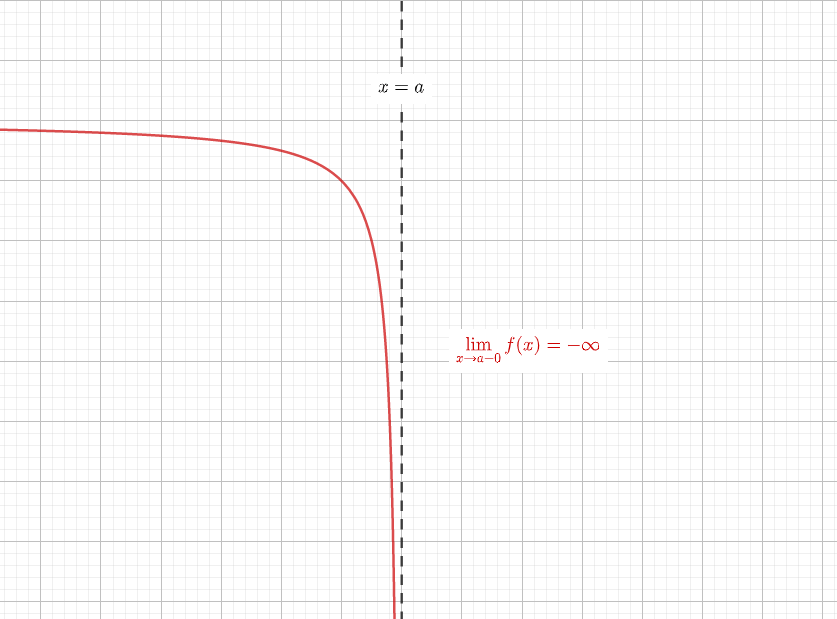
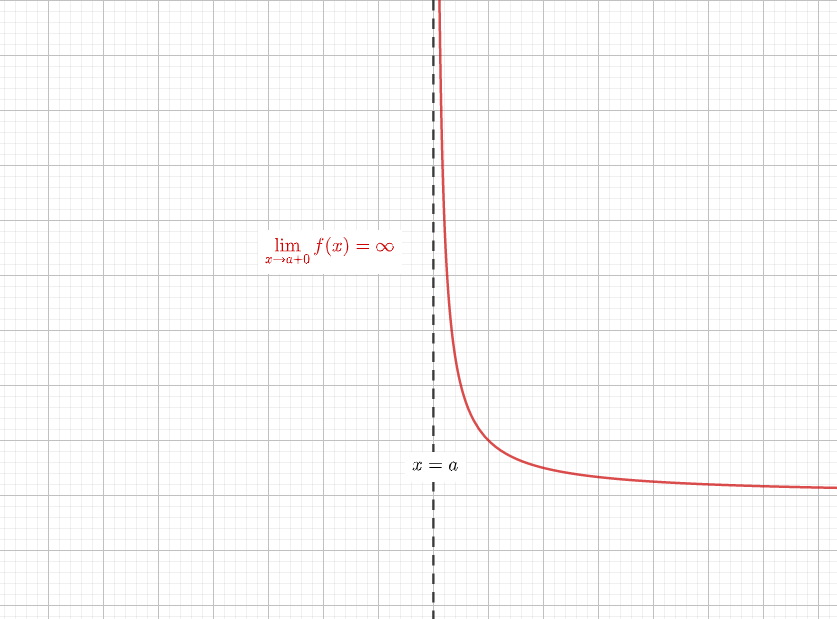
では、反比例の式や値の求め方を見ていきましょう。 例題 yはxに反比例し、x=2のときy=6である。 (1) yをxの式で表しなさい。 (2) x=4のときのyの値を求めなさい。 「yはxに反比例し」ですから、「 y= 」の式を使います。解き方は以下の通りです。 (1):x=2,y=6を y= に代入しaの値を求め、その値を媒介変数表示とx,y方向の変化 → 携帯版は別頁 漸近線の方程式 ※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります② y=f(x)は直線x=1を漸近線として、点(2,3)を通る。 解) しかし、前述の方法ではkの値が分数になると計算が面倒になり、結果はまた計算力に頼る形になってしまうことがある。たとえば、 ex2) 分数関数 の逆関数を求めよ。 解) 漸近線は 。




漸近線の求め方が分かりません 3 です Clearnote



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
Const Range = 18;曲線に対する漸近線の求め方 f (x) = 3x2−5x x−2 f ( x) = 3 x 2 − 5 x x − 2 の漸近線を求めよ。 画像を見ればわかりますが、答えは、 x = 2, y = 3x 1 x = 2, y = 3 x 1 このような問題を解くために、 曲線 y = f (x) y = f ( x) の漸近線が直線 y = ax b y = a x b であるとき 漸近線の求め方 高校 なぜ そんな事を 3334(グラフの準備:漸近線の求め方(指数対数関数)) 3335(y"の正負はグラフの凹凸を表す) 3336(変曲点とy"の符号) 3340(分数関数のグラフ) 3341(グラフの合成②) 3342(三角関数のグラフ) 3343(三角関数のグラフ(y'がcos(x)の多項式)) 3344(無理関数のグラフ) 3345(グラフの合成③) 3350(指数ほかの記事を探す 分野別 レベル別 他 キーワードで検索する 数学の実力を試そう 入試数学コンテスト 物理の記事 高校生から味わう理論物理入門 記事の一覧へ 英




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
漸近線の求め方がこうなる理由がよく分かりません。 下に書いてある証明? はどういう意味なんでしょうか? 04 第6章 微分法の応用 解説 Column コラム 「漸近線」 曲線が限りなく近づいていく直線があるとき, この直線を漸近線という。 これまでに学ん 4つ目の記事 数Ⅲlogを含む関数の漸近線 y=f(x)の漸近線の求め方を先に書いておこう。 ちなみにここで言う漸近線とは「直線」であり、 漸近線を求めることはその直線y=axbの 傾きaと切片bを求めることである。 ①傾きを求める で出てくる値が傾きである。 またそれをaとする。 漸近線の作り方 ビデオ 〔高校数Ⅲ・微分法〕漸近線(y=ax+b タイプ)-オンライン無料塾「ターンナップ」- 21, 10月




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




レナード ジョーンズ ポテンシャルの最小値がなぜ E になるのかわからない Shinshu Univ Physical Chemistry Lab Adsorption Group
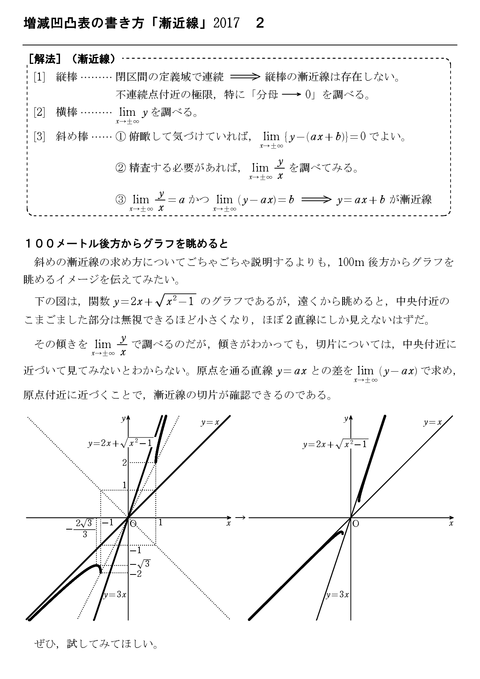
ささ 数3微分のグラフについてです、 この問題の漸近線の求め方が分かりません💧 xを無限に近づけた時の値の求め方はわかりますが、赤線のところがなぜその値なのか理解出来ないです。 どなたかお願いします💧 rs ィベペー1。 1漸近線の方程式 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。 したがって,漸近線の方程式を単独で問うことはまれです。 kを求めた後、xを無限大にする傾向があるので、差の限界f(x) kxを計算してbを決定する必要があります(図3を参照)。 次に、漸近線と直線y = kx bをプロットする必要があります。 5 一例です。 関数y =(x ^ 2 2x1)/(x1)のグラフの漸近線を見つけます。



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
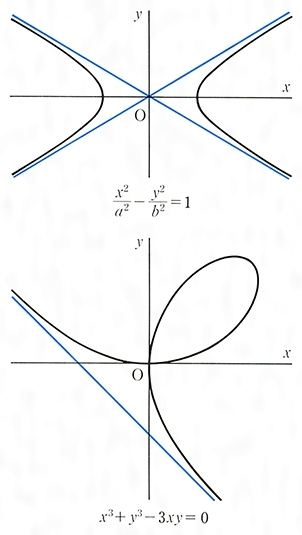
直角双曲線 a = b a = b のときは、先ほど求め双曲線の漸近線は x a − y a = 0, x a y a = 0 x a − y a = 0, x a y a = 0 となります。 これは、書き換えれば、 y = x y = x, y = −x y = − x の2つです。 これらは直交します。 このように、漸近線が直交する双曲線のことを漸近線は 直線 s,\ t である。 2 定義域は s,値域は \ t である。 \ 2 \ 漸近線 定義域 漸近線 値域 グラフは①漸近線をかく ②切片をとる ③象限・漸近線に注意してかく 例1)関数 \ のグラフは, 分母 とすると に変えると とすると \ に変えると \ 関数 \ のグラフを 軸方向に 微分のとこでグラフ描いてるんですけど漸近線の求め方が分からないです。参考書に書いてある $\displaystyle\lim_{x\rightarrow\infty}\{f(x)(axb)\}=0$ ってどういうこと? 確かにパッと見た目じゃ分からないかもね。それ、いったん置いておいて極限のイメージから漸近線作ってみようか。 ad 増減表を




漸近線はy X 2なのになぜこのグラフは漸近線を通っているのですか Clearnote




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
数学・算数 分数関数のグラフの漸近線の方程式について教えてください。 分数関数のグラフの漸近線の方程式について教えてください。 f(x)=2x^2/x^23x2 この関数についてなのです 質問No曲線 漸近線 求め方Double (inflec_pt) ans = 3×1 complex i 136 i 136 i この例では、最初の要素だけがB 距離の差 2 b 双曲線の y 軸との交点の y 座標の値は b, − b この双曲線を表す方程式は 曲線の漸近線について X軸に垂直な漸近線とありますが X軸に垂直な漸近線 Yahoo 知恵袋 ②2つの焦点がy軸上に3 漸近線の求め方 31 軸に平行な漸近線の求め方 32 軸に平行でない漸近線の求め方2STEP 321 STEP1 の極限を調べる→傾きチェック 322 STEP2 代入する 4 漸近線の有無の判別方法 41 チェック① 軸に平行でない漸近線があるか 42 チェック② 不連続な点が



数学iii 怜悧玲瓏 高校数学を天空から俯瞰する



漸近線とは コトバンク
漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) lim漸近線の求め方に関する考察 玉 たま 井 い 克 かつ 樹 き 曲線 =f( ) は を媒介変数とする自然な媒介 変数表示 = , =f( ) をもつので,これを利用 して説明する。以下,f( )は定義域で連続である と仮定する。 例えば,直線 =c が曲線 =f( ) の漸近線に なるとする。曲線 =f( ) 上の点P( ,f( ))が 直線 漸近線 はその直線に向かってグラフが進んでいくが、それを跨ぐことはないというものでした。 もちろん双曲線の一般形でも漸近線があるはずなのですが、その直線は一体何なのでしょうか。 答えだけ言いましょう。与えられた双曲線が \(\displaystyle \frac{x




二次曲線とは 双曲線の方程式の考え方と書き方 高校数学の知識庫



斜めの漸近線について 教えてください 数 のグラフを書く Yahoo 知恵袋
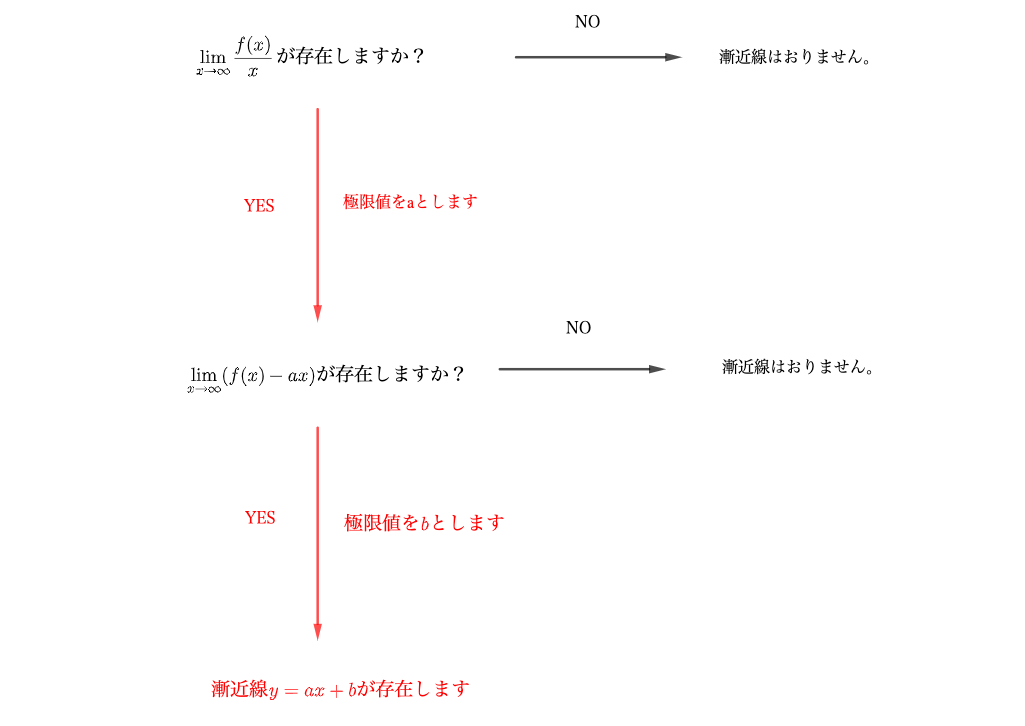
今日は漸近線の求め方について解説します。 漸近線とは曲線が近づく直線のことで 漸近線には3種類あります! ①x軸に平行な漸近線 x→±∞のとき, f(x)→αとなる極限値が存在するとき,,y=αが漸近線となる。 ②y軸に平行な漸近線 x→a±0のとき, f(x)→±∞となるx=aが存在するとき, x=aが漸近線と




漸近線の求め方 高校数学 微分法の応用 14 Youtube



双曲線の焦点についての関係式 C 2 A 2 B 2 ほのぼの数学頑張ろう




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



数学iii 怜悧玲瓏 高校数学を天空から俯瞰する




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



1




漸近線を説明したいけど極限は未習 怜悧玲瓏 高校数学を天空から俯瞰する



漸近線求め方を教えてください なんでこうなるんですか Yahoo 知恵袋




Y Ax B 2x 1 1 のグラフが点 1 0 Okwave



数学 微分の質問です これは漸近線を求めていると思うのですが なぜ 漸近線 Yahoo 知恵袋



斜めの漸近線について 教えてください 数 のグラフを書く Yahoo 知恵袋




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す




漸近線の求め方が分かりません 3 です Clearnote




漸近線 問題編 1 数 微分法 現大手予備校講師の5分でわかる 高校数学 Youtube




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋




漸近線はy X 2なのになぜこのグラフは漸近線を通っているのですか Clearnote
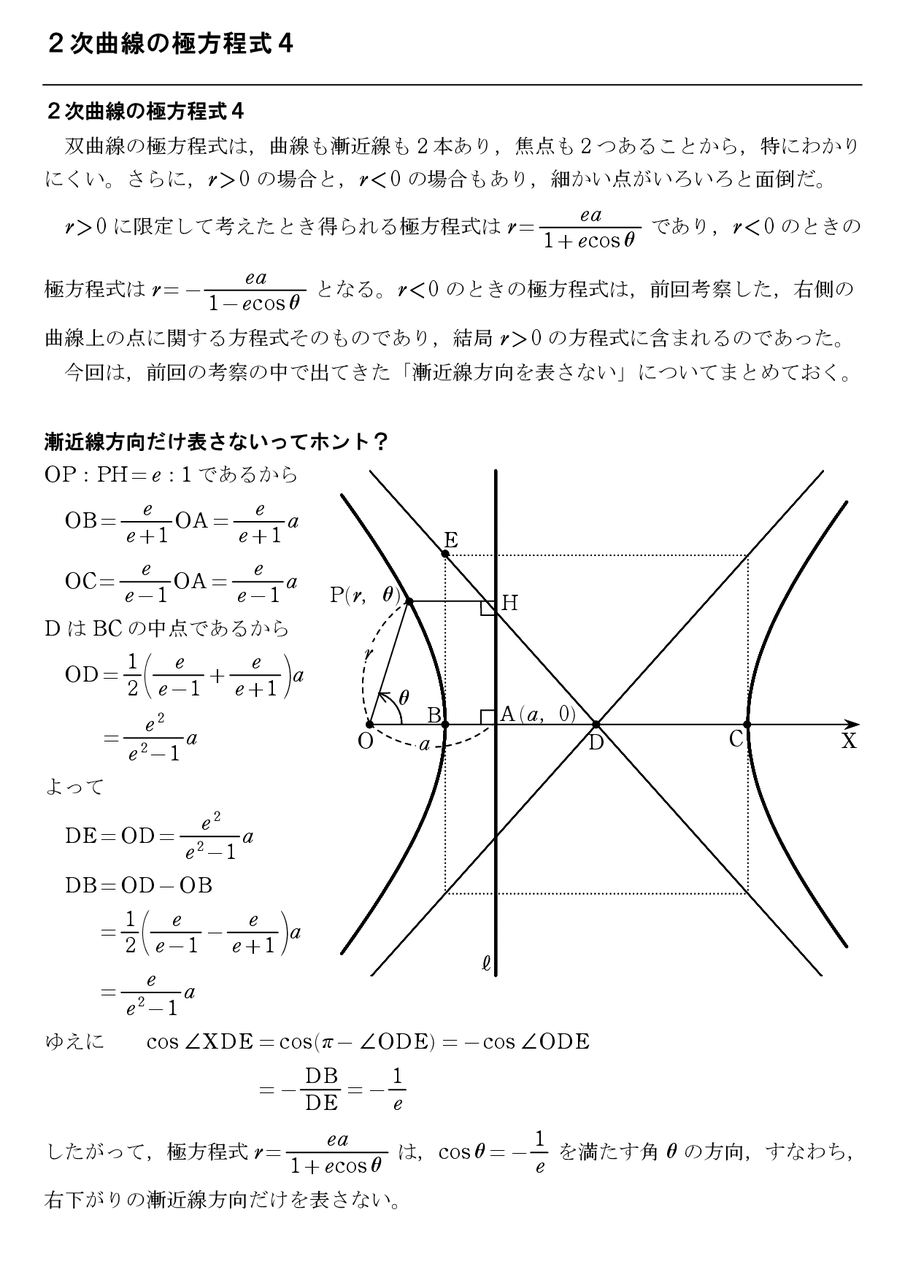



ええと なぜ8と28なんでしょうか 怜悧玲瓏 高校数学を天空から俯瞰する



2
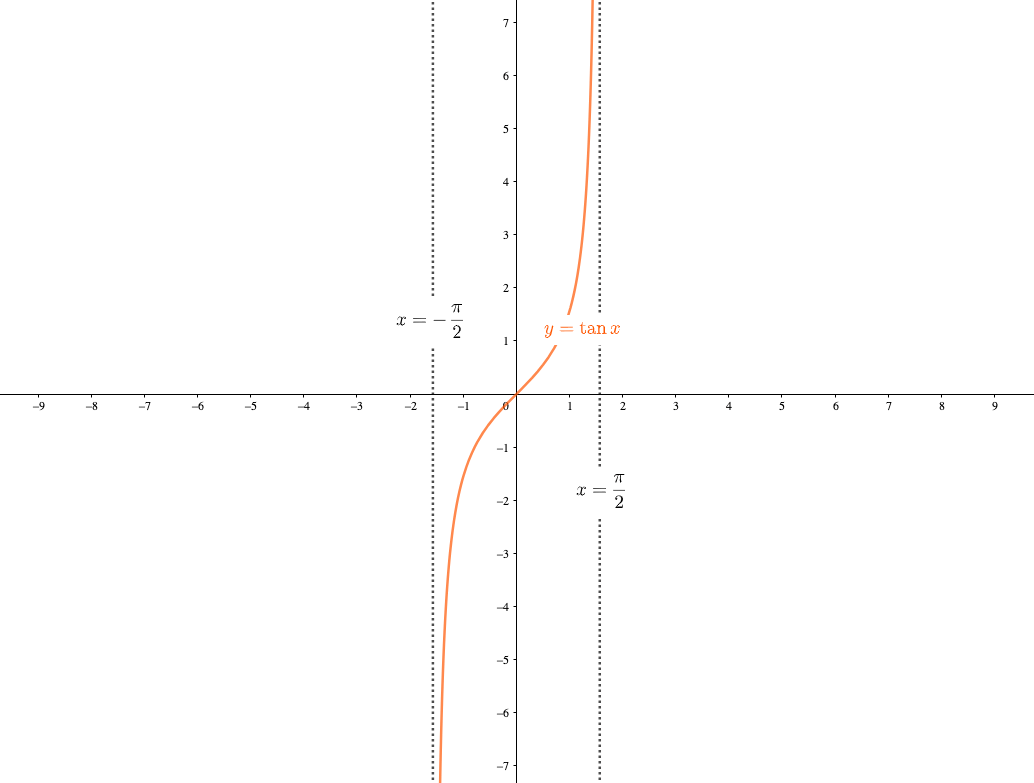



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語



漸近線って 本当に超えないんですか 高校数学の質問です Yahoo 知恵袋




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




数3微分のグラフについてです この問題の漸近線の求め方が分かりません Clearnote



高校数学漸近線数3青チャート 画像の問題の 2 の解答の2行目のとこ Yahoo 知恵袋




数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube




漸近線の求め方がこうなる理由がよく分かりません 下に書いてある証明 はどうい Clearnote



数3の漸近線の求め方について X軸に平行なもの 垂直なもの 平行でも垂直で Yahoo 知恵袋




高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典




数 微分法 漸近線 Y Ax B タイプ オンライン無料塾 ターンナップ Youtube



高校数学の数3の漸近線の求め方なのですが なぜ括弧の中のような事 Yahoo 知恵袋
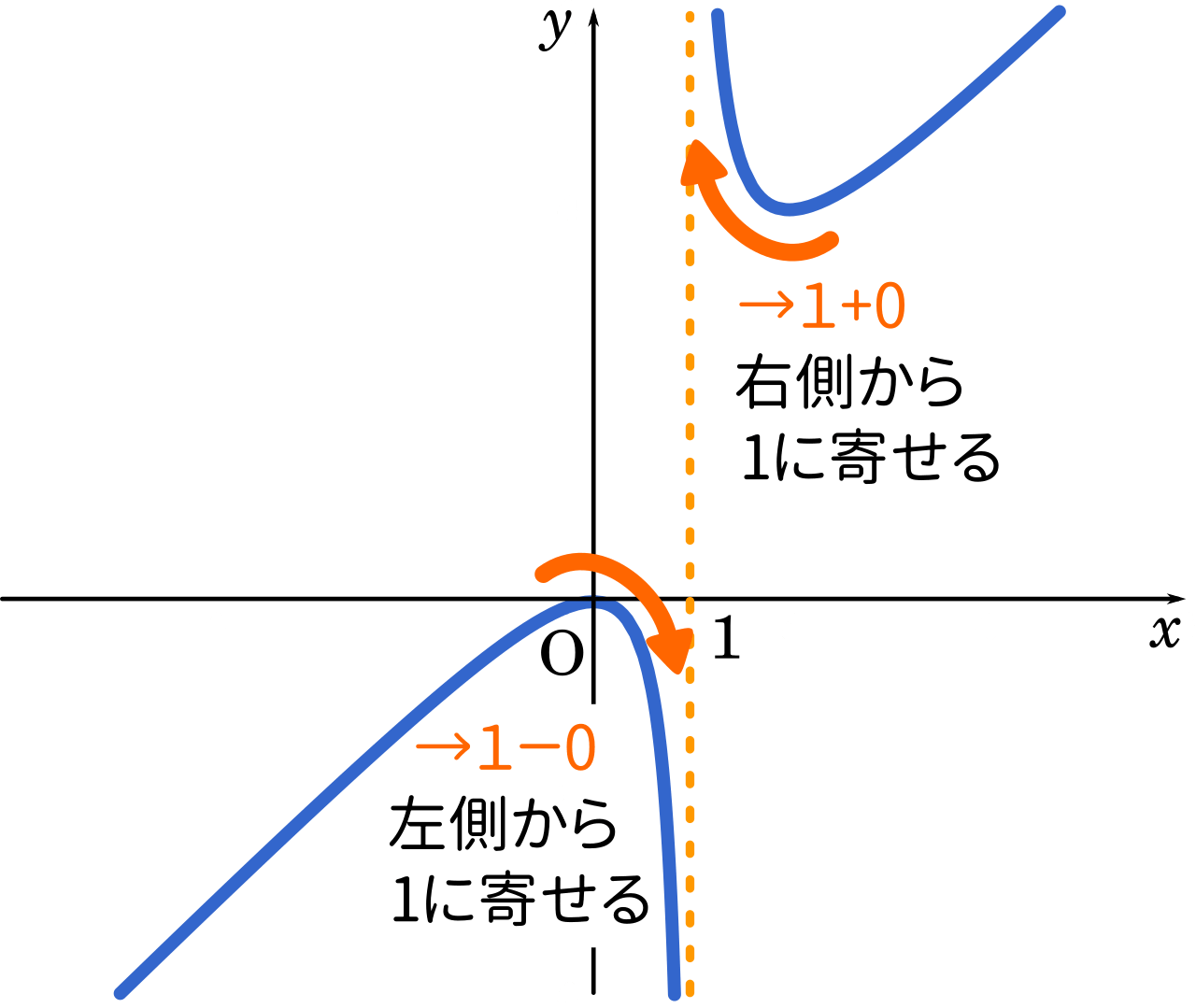



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書




Y Tan8のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア



高校数学数lllの問題です 傾きのある漸近線の求め方がわかりません 例 Yahoo 知恵袋
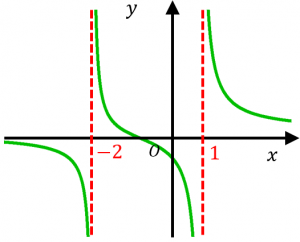



漸近線の求め方3パターン 具体例で学ぶ数学



1



漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
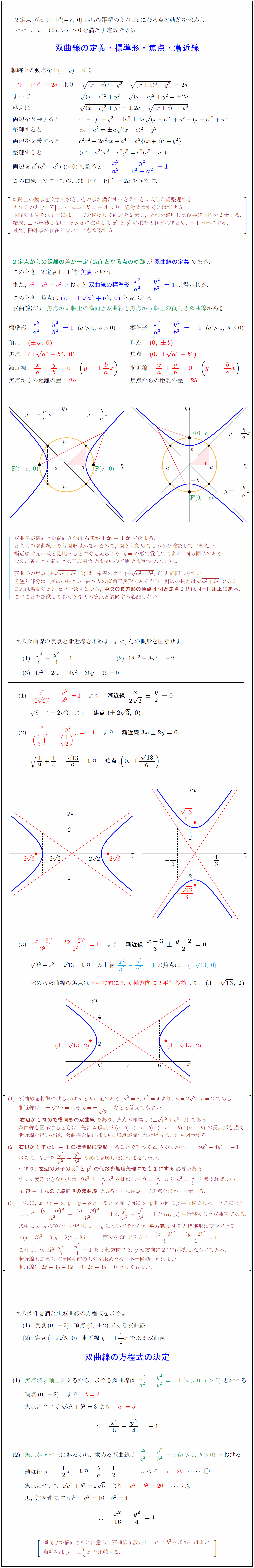



高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




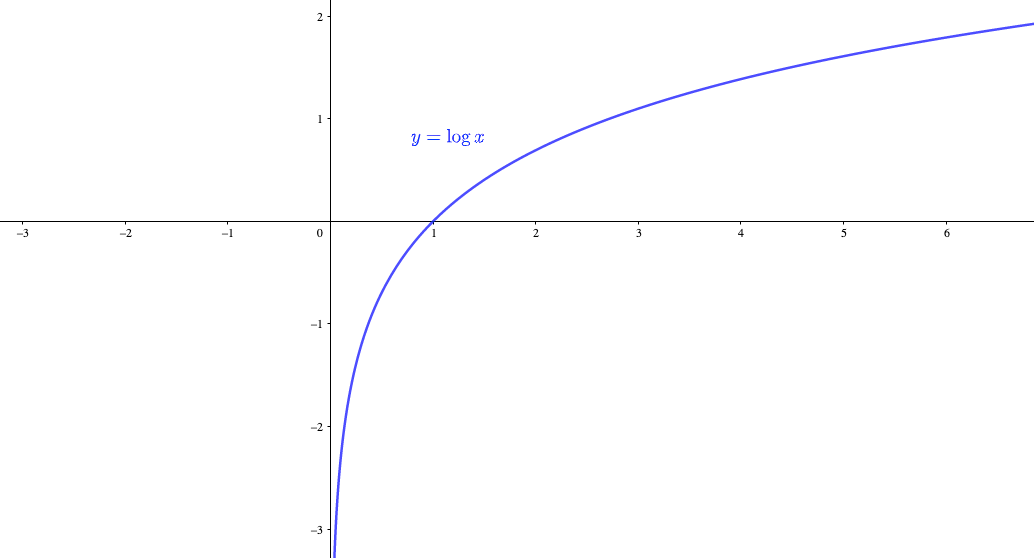
対数関数の漸近線の求め方がわかりません Clearnote




基本 双曲線と漸近線 なかけんの数学ノート




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




漸近線の求め方が分かりません 3 です Clearnote
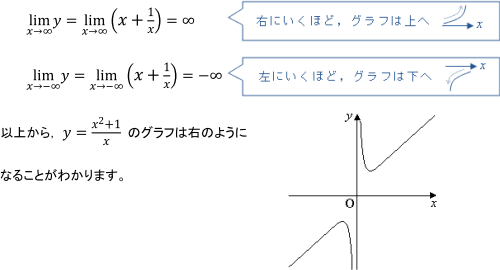



複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ
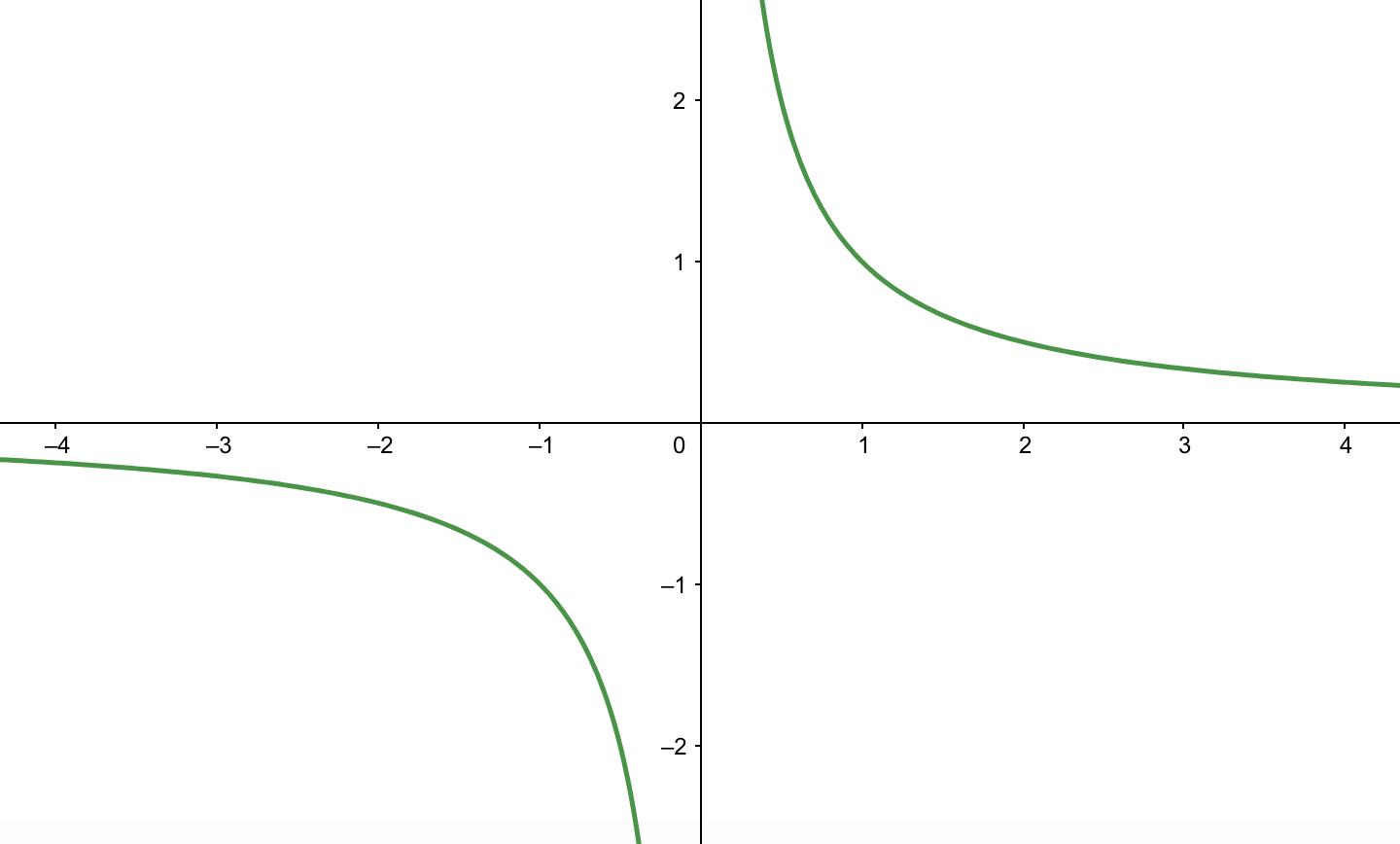



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



1



極限を使っての漸近線の求め方についてです なぜ無限大や0に近づけ Yahoo 知恵袋




Y Tan 28 P 2 のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア
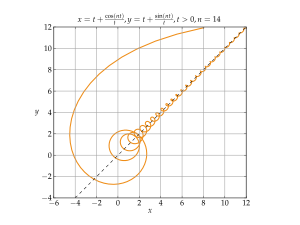



漸近線 Wikipedia




Mgujwsla Zwobm



漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋



X 0で漸近線とる理由とy X X分の1にして漸近線とる理由教えて欲しいです Yahoo 知恵袋



正規分布の話ですが 正規分布曲線はx軸が漸近線で 確率は面積に等しい なのに Yahoo 知恵袋



漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋




漸近線の方程式がy 2x 5 Y 2x 3で 点 1 1 を通る双曲線の方程式を その他 教育 科学 学問 教えて Goo
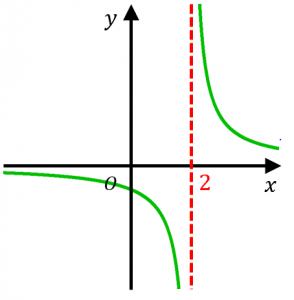



漸近線の求め方3パターン 具体例で学ぶ数学



双曲線の方程式




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




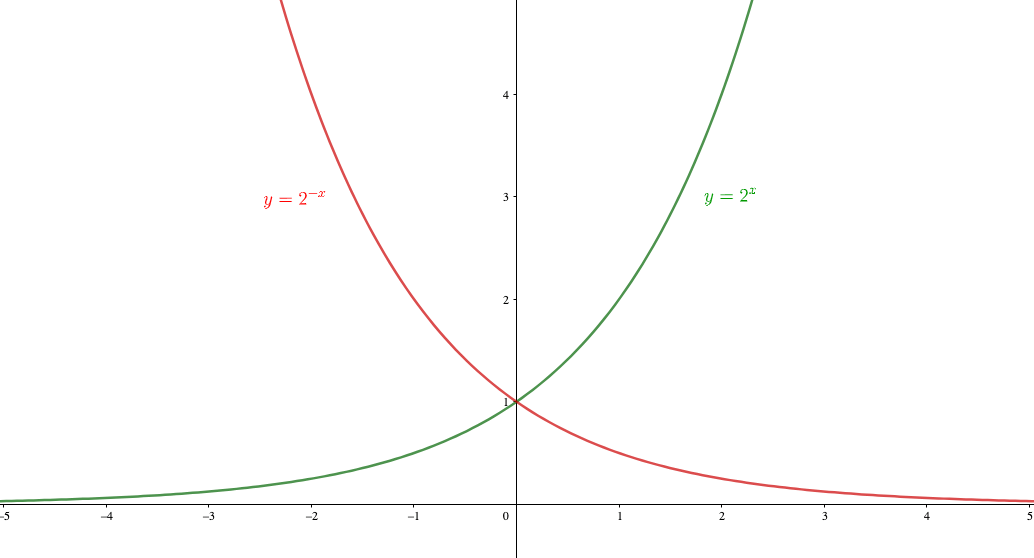
指数関数とは何か 指数と関数の意味からわかるグラフの仕組みとその性質 アタリマエ




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ




あやは 勉強垢 Iama Student Twitter




標準 微分と関数のグラフと漸近線 なかけんの数学ノート




漸近線 Wikipedia
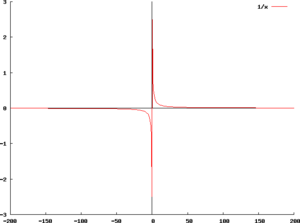



漸近線 Wikipedia




漸近線の求め方がこうなる理由がよく分かりません 下に書いてある証明 はどうい Clearnote



どうして 中心が原点 漸近線の傾きが 2で 点 1 2 0 を通 Yahoo 知恵袋
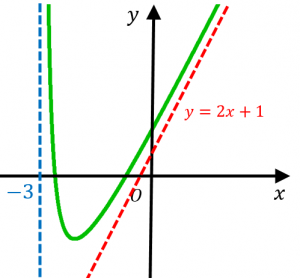



漸近線の求め方3パターン 具体例で学ぶ数学




漸近線 身勝手な主張



漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋




漸近線の求め方が分かりません 3 です Clearnote



どうして 中心が原点 漸近線の傾きが 2で 点 1 2 0 を通 Yahoo 知恵袋




Mgujwsla Zwobm



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




数学3です なぜy Xが漸近線だといえるのでしょうか Clearnote
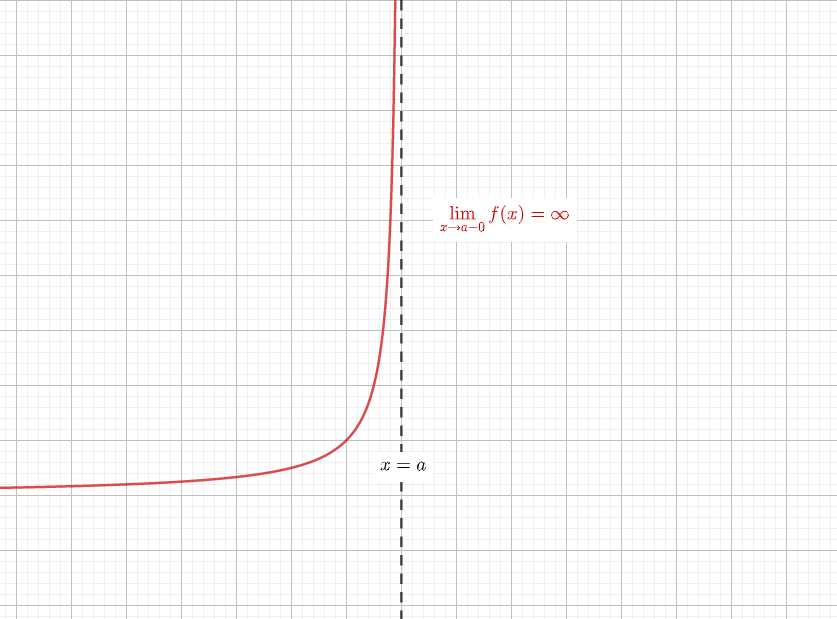



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



0 件のコメント:
コメントを投稿